Auf vielfachen Wunsch [:-)] kommt hier nochmal Teil 2. Der Magdeburger Server wurde gerade umkonfiguriert, als ich diesen Teil deponiert habe, was offenbar dazu fuehrte, dass er ausser in Magdeburg kaum wo zu lesen war. Ich selbst habe ihn jedenfalls in Stuttgart nicht sehen koennen...
Uebrigens fuer die, die die Conclusio kaum mehr erwarten koennen: das Machwerk wird insgesamt 5 Teile haben und der letzte wird weniger oder gar keine Bilder enthalten...
Im letzten Abschnitt des Kurses haben wir gesehen, wie aus der Gueltigkeit des Relativitaetsprinzips plus der Konstanz der Vakuumlichtgeschwindigkeit folgt, dass Gleichzeitigkeit keine absolute Bedeutung hat, sondern beobachterabhaengig ist. Hier sollte man noch anfuegen, dass -- im Rahmen der speziellen Relativitaetstheorie -- die Gleichzeitigkeit eines Beobachters mit konstantem Bewegungszustand durchaus relativ ist. Das heisst, der "schwarze" Beobachter kann feststellen, dass die Ereignisse A und B im damals gezeigten Bild lorentz_2 fuer den "blauen" Beobachter gleichzeitig sein muessen (auch wenn sie es fuer ihn selbst nicht sind). Es besteht also keine subjektive Beliebigkeit.
Noch eine Anmerkung: die Raum-Zeit-Diagramme zur Veranschaulichung der Lorentz-Transformationen nennt man Minkowski-Diagramme.
3.2 Massstaebe
In der ersten Lektion hatte ich gesagt, dass man bei schiefwinkligen Koordinatensystemen immer ein bisschen achtgeben muss, wie Massstaebe definiert sind. Im Fall der Galilei-Transformation erhielten wir den Zeitmassstab unter Ausnuetzung der Absolutheit der Newtonschen Zeit. Der Raummassstab war fuer beide Beobachter derselbe.
Im Fall der Lorentz-Transformationen muss man anders vorgehen. Was man braucht, um Massstaebe festlegen zu koennen, ist eine Kurve (Hyperflaeche), die in beiden Koordinatensystemen dieselbe ist; der technische Ausdruck ist, dass sie invariant unter der Koordinatentransformation ist.
 |
| Bild lorentzhyp |
|---|
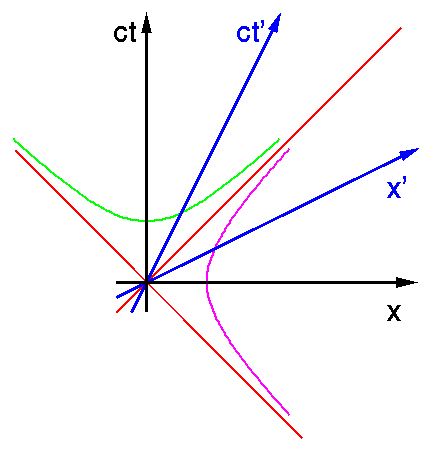
Einen Typ solcher Kurven kennen wir bereits: die Weltlinien von Licht, im Bild lorentzhyp rot gezeichnet. Sie sehen fuer beide Beobachter exakt gleich aus. Diese Weltlinien nennt man Lichtkegel und zwar den Teil oberhalb der " Gegenwart" Vorwaertslichtkegel, den in der Vergangenheit liegenden Rueckwaertslichtkegel.
Zur Massstabsfestlegung kann man andere invariante Kurven verwenden, naemlich Hyperbeln, deren Asymptoten gerade auf dem Lichtkegel liegen. Wie man ohne Mathematik zeigen kann, dass solche Kurven invariant sind, weiss ich nicht. Wenn jemand eine gute Idee hat -- ich bin interessiert. Dass diese Hyperbeln invariant sind, setzen wir hier also ohne Beweis voraus.
Was ihre Invarianz bedeutet, ist dann wieder einfach. Die gruene Hyperbel, die die Zeitachsen schneidet, tut das fuer beide Beobachter im selben Abstand. Die Zeitintervalle von t=0 zum Schnittpunkt der Hyperbel mit der ct-Achse und von t'=0 zu ihrem Schnittpunkt mit der ct'-Achse sind also gleich lang! Damit koennen wir einen Zeitmassstab einfuehren. Wir legen ein Zeitintervall von 1 Sekunde im (xt)-System fest und konstruieren die Hyperbel, die bei t=1 Sek. die ct-Achse senkrecht schneidet und deren Asymptoten durch den Lichtkegel gegeben sind. Dann ist der Schnittpunkt mit der ct'-Achse bei t' = 1 Sekunde.
Voellig analog verfaehrt man mit Laengen. Schneidet die magentafarbene Hyperbel die x-Achse bei x = 1 m, so ist ihr Schnittpunkt mit der x'-Achse bei x' = 1 m.
Mit diesem Wissen ausgeruestet, koennen wir mehr als die blosse Gleichzeitigkeit diskutieren (dafuer reichte die Parallelprojektion). Wir koennen gemessene Zeit- und Laengenintervalle in den beiden Systemen vergleichen.
3.3 Die Zeitdilatation
 |
| Bild timedilat1 |
|---|
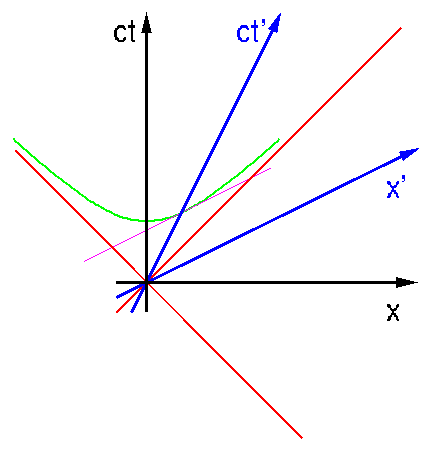
Nehmen wir mal an, der schwarze und blaue Beobachter haben, als sie sich trafen (das ist das Ereignis " Koordinatenursprung von Bild timedilat1"), ihre Uhren auf dieselbe Zeit gestellt, um konkret zu sein, auf 12:00 Uhr.
Eine Stunde spaeter, also um 1:00 Uhr auf seiner Uhr, will der blaue Beobachter wissen, wie spaet es gerade bei dem schwarzen ist. Um das rauszukriegen, muss er bloss feststellen, wann die Parallele zu seiner x'-Achse (eine Linie gleicher Zeiten) die ct-Achse schneidet. Offensichtlich tut sie das zu einer Zeit, die vor dem Schnittpunkt der gruenen Massstabshyperbel mit der ct-Achse liegt. (Die Parallele ist Tangente an die Hyperbel.)
Also schliesst der blaue Beobachter, dass um 1:00 Uhr bei dem schwarzen noch nicht 1:00 Uhr ist; das heisst, die Zeit des schwarzen Beobachters laeuft langsamer. Sie dehnt sich gewissermassen, um das kuerzere Intervall auf das laengere (von 1 Stunde Dauer) auszudehnen, daher der Name Zeitdilatation.
 |
| Bild timedilat2 |
|---|
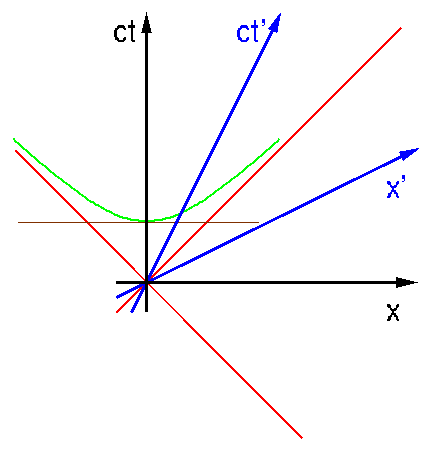
Nun wollen wir uns anschauen, wie die Dinge aus der Sicht des schwarzen Beobachters liegen; dazu werfen wir einen Blick auf Bild timedilat2. Er schaut um 1:00 Uhr auf seine Uhr und ueberlegt sich, wie spaet es jetzt wohl bei dem blauen Beobachter ist. Na ja, nichts leichter als das: waagerechte Tangente an die Massstabshyperbel, was zeigt, dass es bei dem blauen Beobachter noch nicht 1:00 Uhr ist. Also geht die Zeit des blauen langsamer. Na ja, nichts besonderes; das ist eben die Zeitdilatation.
Hoppla, kann das denn stimmen? Jeder der beiden Beobachter stellt fest, dass die Zeit des anderen langsamer geht. Nach dem Relativitaetsprinzip kann es nicht anders sein, denn sonst koennte man ein Bezugssystem auszeichnen und " ruhend" nennen -- es waere das, in dem die Zeit am schnellsten geht. Andererseits widerspricht die Idee, dass, wenn die Zeit des anderen aus meiner Sicht langsamer geht, meine eigene Zeit aus dessen Sicht nicht schneller geht, sondern auch langsamer, doch sehr der Intuition.
Aber ein echter Widerspruch entsteht natuerlich nicht. Dass jeder feststellen kann, dass die Zeit des anderen langsamer geht als die eigene, liegt natuerlich daran, dass die Gleichzeitigkeiten der beiden verschieden festgelegt sind. Gaebe es eine absolute Gleichzeitigkeit, waere eine solche Folgerung in sich widerspruechlich. Es kann nicht, wenn es bei dem einen 1:00 Uhr ist, beim anderen gleichzeitig vor und nach 1:00 Uhr sein. Aber es kann sehr wohl mit der Gleichzeitigkeit des schwarzen Beobachters nach 1:00 Uhr sein, wenn es auf der Uhr des blauen genau 1:00 Uhr ist (Bild timedilat2), und mit der Gleichzeitigkeit des blauen Beobachters vor 1:00 Uhr beim schwarzen, wenn es bei ihm 1:00 Uhr ist (Bild timedilat1). Die Absolutheit der Zeit ist eben aufgehoben.
3.4 Die Laengenkontraktion (Lorentz-Kontraktion)
 |
| Bild lengthmeasure1 |
|---|
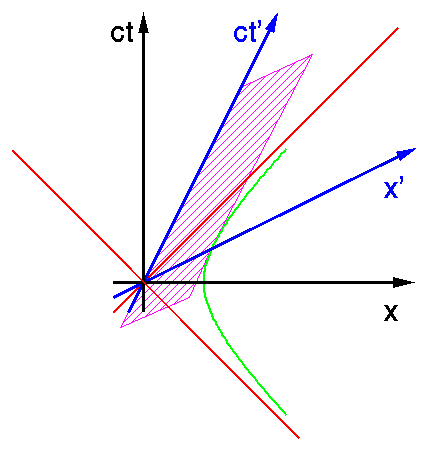
Das naechste Bild (lengthmeasure1) befasst sich mit der Frage von Laengenmessungen.
Das schraffierte Parallelogramm stellt die Weltlinien eines im blauen System ruhenden Meterstabs dar. Wie lang ist dieser Stab im schwarzen System?
Die Frage ist a priori gar nicht so einfach zu beantworten. Denn im schwarzen System bewegt sich der Stab ja. Versucht man also, seine Laenge mit einem Massband zu messen, so wird eine gewisse Zeit zwischen dem Anlegen des Massbands an seinem einen Ende und dem Erreichen des anderen Endes vergehen, das sich inzwischen aber weiterbewegt hat. Der gemessene Abstand der beiden Enden ist dann natuerlich nicht die Laenge des Stabs. Um die wirkliche Laenge herauszubekommen, muss man also die Position der beiden Enden zu einem Zeitpunkt kennen. Das kann man etwa erreichen, indem man eine Menge Beobachter (die relativ zum schwarzen System ruhen) entlang der x-Achse aufstellt; die beiden Beobachter, bei denen zur Zeit t=0 ein Stabende ist, ritzen dort, wo es sich befindet, eine Kerbe in den Boden. Dann kann man in aller Ruhe den Abstand der beiden Kerben messen. Wenn aber die Laengenbestimmung so eng mit der Zeitbestimmung verknuepft ist, nimmt es nicht weiter wunder, dass verschiedene Beobachter zu verschiedenen Resultaten kommen.
So ist es auch. Man kann dem Bild sofort entnehmen, dass die beiden Schnittpunkte der Weltlinien der Stabenden mit der x-Achse näher beeinander liegen als die Stabenden im (x' t')-System; denn der Abstand 1 m vom Ursprung ist ja durch die gruene Hyperbel bestimmt. Der bewegte Massstab ist also im schwarzen System kürzer als im blauen, deshalb spricht man von Laengenkontraktion.
Angenommen, die Verkuerzung reduziert die Laenge des Stabs im schwarzen System auf 80 cm. Wenn wir dann zu dem Zeitpunkt (im schwarzen System), zu dem sein eines Ende den Ursprung (x=0, t=0) passiert, entlang der gesamten x-Achse mit Ausnahme eines "Lochs", das von x=-5cm bis x= 85cm geht, Laserstrahlen zuenden (die z.B. parallel zur nicht gezeichneten y-Achse laufen), so wird der Stab das Loch ohne weiteres durchfliegen, da er ja kuerzer als 90cm ist. Die Laserstrahlen sollen unmittelbar danach wieder abgeschaltet werden.
 |
| Bild lengthmeasure2 |
|---|
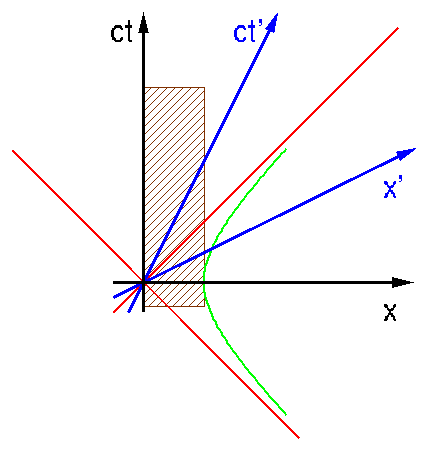
Nun sehen wir uns eine aehnliche Situation an, bei der ein Stab im (xt)-System ruht (Bild lengthmeasure2). Seine Laenge im blauen System, gegeben durch die Schnittpunkte mit der x'-Achse, ist offenbar ebenfalls kürzer als die Laenge im schwarzen System. Wir haben also wieder eine symmetrische Situation. Jeder Beobachter stellt fest, dass Laengen im anderen System kuerzer sind als im eigenen.
Gibt das mit unserem Loch in einer Wand aus Laserstrahlen kein Problem? Vom bewegten Stab aus, der sich im blauen System befindet (Bild lengthmeasure1), ist seine eigene Laenge ja 1 m, die des Lochs sollte hingegen kuerzer sein als die 90 cm, die im schwarzen System gemessen werden... Die Laserstrahlen sollten also die Enden des zu langen Stabs abschneiden...
Das waere in der Tat eine paradoxe Situation. Aber so ist es natuerlich nicht. Denn fuer den Stab im blauen System (Bild lengthmeasure1) zuenden die Laserstrahlen nicht gleichzeitig. Was aus seiner "Sicht" passiert, ist, dass die Laserstrahlen fuer sehr grosse x-Werte sehr frueh zuenden. Dann naehert sich die Laserfront (ueberlichtschnell!) bis kurz vor dem Zeitpunkt, zu dem sein Vorderende die x-Achse passiert. Dann gehen die Laser aus und nach einer Pause auf der negativen x-Achse wieder an, von wo sich die Laserfront zu negativen x-Werten hin entfernt. Die Laser gehen aber erst an, nachdem das Hinterende des Stabs die x-Achse passiert. Zu diesem Zeitpunkt ist sein Vorderende dort, wo vorher Laserstrahlen waren. Das heisst, der Stab ist wohl laenger als der kuerzeste Abstand der Laserfeuer, aber sein Vorderende geht vor seinem Hinterende durch das "Loch" und zwar gerade so, dass es die Laser vermeidet.
Vom blauen System aus gesehen, ist gar kein raeumliches Loch da, sondern nur eine Laserfront, die ausgeht, knapp bevor sie passiert wird und wieder an, nachdem man vorbei ist.
So ist auch Minkowskis Zitat zu verstehen, "Raum fuer sich selbst und Zeit fuer sich selbst werden in blosse Schatten versinken, und nur eine Art Vereinigung zwischen ihnen wird ueberleben": das Loch, das im einen System eine rein raeumliche Distanz verkoerpert, ist im anderen eine Kombination aus einer (kuerzeren) raeumlichen und einer zeitlichen Distanz.
Damit soll's fuer heute genug sein. Beim naechstenmal werde ich zeigen, dass die Lorentzkontraktion gar nicht wie eine Kontraktion aussieht und das Zwillingsparadoxon erlaeutern. Und dann geht es an die Science fiction.
Klaus Kassner
Institut fuer Theoretische Physik / Computerorientierte Theor. Physik
Otto-von-Guericke-Universitaet Magdeburg
Postfach 4120 / D-39016 Magdeburg