Beim letzten Mal haben wir uns klargemacht, wie aus dem Zusammenwirken von Relativitaetsprinzip und Konstanz der Vakuumlichtgeschwindigkeit die Effekte der Zeitdilatation und der Laengenkontraktion folgen.
Nun kommt es schon mal vor, dass ein "Relativist" ein bisschen darauf herumreitet, dass die Laengenkontraktion nur eine Folge unserer Konventionen zum Laengenmessen sei. So ganz und gar falsch ist das nicht, denn wenn wir uebereinkaemen, Laengen bewegter Objekte nicht als " Laengen zu einer festen Zeit" zu messen, so haetten wir nicht notwendigerweise eine relativistische Laengenkontraktion. Aber es ist eigentlich keine andere vernuenftige Konvention zu sehen (Konventionen moegen beliebig sein, aber ihre Nuetzlichkeit haengt sehr wohl von ihrem Inhalt ab). Und es folgt aus der Abhaengigkeit der Laengenkontraktion von der Messvorschrift fuer Laengen eben nicht, dass sie irgendwie nicht real sei.
Das zeigt sehr schoen das Raumschiffparadoxon von John Bell (ja, dem beruehmten, der die Bellschen Ungleichungen abgeleitet hat):
Man stelle sich zwei Raumschiffe vor, die bezueglich eines festen Beobachters exakt das gleiche Beschleunigungsprogramm haben, so dass ihr Abstand gleich bleibe. Zwischen den Raumschiffen sei ein Seil gespannt, das genau die Laenge ihres Abstands hat. Es soll kein besonders starkes Seil sein, so dass es die Beschleunigungen der Raumschiffe nicht beeinflusst.
Reisst das Seil oder reisst es nicht? Dafuer, dass es nicht reisst, spricht, dass seine Laenge fest bleibt. Dafuer, dass es reisst, spricht, dass es ja eigentlich eine Lorentzkontraktion machen muesste. Dieses Puzzle wurde von Kennern der Relativitaetstheorie auch schon falsch geloest (auf die Schnelle, im nachhinein verstehen sie es dann schon). Die Antwort kommt in der naechsten Kurseinheit.
Dieses Beispiel ist auch geeignet klarzumachen, dass die spezielle Relativitaetstheorie nicht auf Objekte beschraenkt ist, die sich mit konstanter Geschwindigkeit bewegen. Man kann durchaus beschleunigte Systeme damit behandeln. Die Beschreibung innerhalb der Theorie erfolgt aus der Sicht eines unbeschleunigten Beobachters. Das heisst, sie beschreibt physikalische Phaenomene, wie sie in Inertialsystemen beobachtet werden. Das sind unbeschleunigte Bezugssysteme. Alle solchen Systeme haben relativ zueinander konstante Geschwindigkeiten (solange keine Gravitation ins Spiel kommt, und die wird von der speziellen Relativitaetstheorie nicht beschrieben). In gewisser Weise kann man sagen, dass eine wesentliche Aussage der speziellen Relativitaetstheorie die Existenz solcher Inertialsysteme ist.
Will man die physikalische Gesetzmaessigkeiten, die ein beschleunigter Beobachter feststellt, aus der speziellen Relativitaetstheorie ableiten, so ist immer Vorsicht angebracht. Das Unterfangen ist nicht unmoeglich, denn letztlich ist die allgemeine Relativitaetstheorie (mit einigen Zusatzannahmen) so gefunden worden.
Doch nun weiter mit der Physik.
3.5 Die Unsichtbarkeit der Lorentzkontraktion
In einer Geschichte zur Veranschaulichung der Laengenkontraktion (von George Gamov: Mr. Thompkins seltsame Reisen durch Kosmos und Mikrokosmos) wird der Held in eine Welt versetzt, in der die Lichtgeschwindigkeit nur 30 km/s betraegt. Folglich sieht er die Radfahrer verkuerzt und, als er selbst eine Zugfahrt macht, sehen alle Haeuser um ihn herum verkuerzt aus. Roman Sexl schreibt dann einen Nachsatz: "Was der Professor noch nicht wusste... "
Es ist naemlich so, dass die Laengenverkuerzung sich auf die tatsaechliche Laenge zu einer Zeit bezieht. Wenn wir einen ausgedehnten Gegenstand betrachten, sehen wir seine verschiedenen Teile aber gerade nicht, wie sie zu einer Zeit aussehen, sondern wir sehen weiter entfernte Teile, wie sie frueher waren als naeher liegende.
 |
| Bild lorentzunseen |
|---|
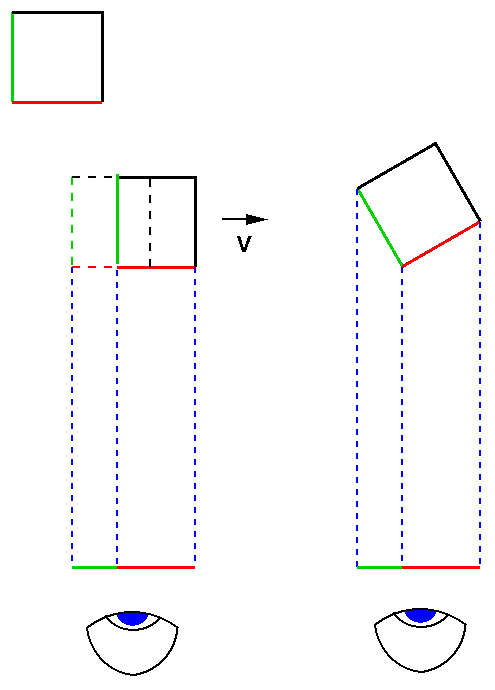
Das veranschaulicht das Bild lorentzunseen. Links oben haben wir ein Quadrat, dessen linke Seite gruen, die untere rot angemalt ist.
Dieses Quadrat bewege sich mit einer konstanten Geschwindigkeit v nach rechts. Dabei wird es natuerlich in der Richtung von v lorentzverkuerzt. Die rote Seite wird kuerzer. Die gruene aendert sich nicht.
Der Beobachter, dessen Auge unten gemalt ist, sieht also nach der Zeit, die das Licht von der roten Seite aus braucht, um bis zu ihm zu gelangen, die verkuerzte rote Seite. Aber, und das ist der springende Punkt, er sieht auch die gruene Seite, denn in der Zeit, die das Licht von der linken oberen Ecke des Quadrates zur linken unteren braucht, hat sich dieses ja weiterbewegt, und so kommt Licht von allen gruenen Punkten des Quadrates (ausgesandt zwischen der Zeit, in der das Quadrat die gestrichelte Lage einnahm und der, in der es die Lage mit den durchgezogenen Strichen hat) zu seinem Auge. Er sieht also von dem Quadrat einen gruenen und einen roten Strich.
Rechts ist dargestellt, was der Beobachter von einem ruhenden aber gedrehten Quadrat sehen wuerde. Was dieses Bild suggeriert, ist richtig: der optische Eindruck ist derselbe, vorausgesetzt, man waehlt den richtigen Drehwinkel (er ist durch sin{\phi} = v/c gegeben).
Die Lorentzkontraktion wird optisch also nicht als Kontraktion sondern als Drehung wahrgenommen! Eine Kugel etwa behaelt Kugelgestalt. Damit ist die Kontraktion als solche unsichtbar.
3.6 Das Zwillingsparadoxon
Eine Diskussion der speziellen Relativitaetstheorie waere ohne das Zwillingparadoxon unvollstaendig. Hier kommt es: Theresa und Stella sind Zwillinge, wobei Theresa einen etwas bodenstaendigeren Charakter hat, mehr auf Terra verwurzelt ist, waehrend es Stella zu den Sternen zieht. Und sie nimmt die erste Gelegenheit wahr, um mit Mr. Ypsilon, der ein Raumschiff erproben will, nach Alpha Centauri zu fliegen, das sich ca. 4 Lichtjahre. Das Raumschiff wird praktisch dauernd mit 4/5 der Lichtgeschwindigkeit fliegen, was, wenn man es nachrechnet, einen Zeitdilatationsfaktor von 3/5 gibt. Die Reise dauert also aus der Sicht von Y und Stella statt 5 nur 3 Jahre. Wenn sie zurueckkommt, ist sie nur 6 Jahre aelter als vorher, Theresa aber 10. Theresa grollt, als sie das hoert.
 |
| Bild zwilling1 |
|---|
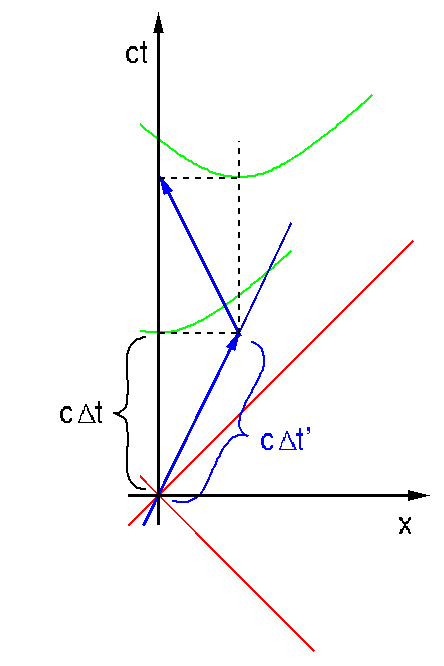
Das Diagramm zwilling1 macht die Situation klar. Stella bewegt sich entlang der durch die blauen Pfeile gegebenen Trajektorie. Auf der Erde vergeht zweimal die Zeit \Delta t, bis sie zurueckkommt, waehrend fuer Stella zweimal die Zeit \Delta t' ablaeuft, und die Massstabshyperbeln zeigen ganz klar, dass \Delta t' kleiner ist als \Delta t.
Nun ist Theresa aber nicht dumm. Sie weiss, dass sich ja die Erde bezueglich des Raumschiffs bewegt, folglich muss aus Stellas Sicht natuerlich waehrend jedes der beiden Fluege Theresa langsamer altern als Stella. Also wird sie selbst bei Stellas Rueckkehr die juengere sein!
Wenn es tatsaechlich so waere, haetten wir ein ernstes Problem: Denn nach der Rueckkehr koennen die beiden ihre Alterungserfahrungen (oder ihre Kalender) wirklich vergleichen, und es ist nicht gleichzeitig moeglich, dass auf dem Kalender von Theresa weniger Tage abgehakt sind als auf dem von Stella und dass auf dem von Stella weniger Tage abgehakt sind als auf dem von Theresa. Das waere echt paradox, in sich widerspruechlich. Und jedes Paradoxon muss ja seine Aufloesung darin finden, dass es sich als nur scheinbar paradox erweist.
 |
| Bild zwilling2 |
|---|
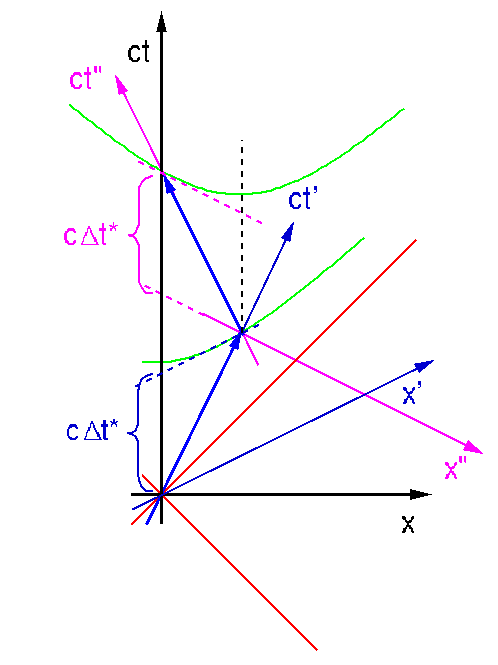
Nun, Stella laesst sich auch nicht ins Bockshorn jagen. Sie hat laengst aufgezeichnet, wie der Flug aus ihrer Sicht aussieht. Das ist das Diagramm zwilling2. Waehrend des Fluges in Richtung Centaurus vergeht fuer Theresa die Zeit \Delta t*, die tatsaechlich kuerzer ist als \Delta t', wie wieder die Massstabshyperbel beweist. Waehrend des Rueckfluges ist es ebenso. Aber: die beiden Zeiten schliessen sich nicht unmittelbar aneinander an, dazwischen ist eine Luecke! Denn Stella wechselt das Inertialsystem. Sie geht beim Umkehren ueber vom Bezugssystem (x' t') zum System (x" t"). Waehrend des Umkehrvorgangs altert aus ihrer Sicht Theresa unheimlich schnell. Nach dem Umkehren altert sie wieder langsamer als Stella (aber sie holt den Zeitverlust bis zur Rueckkehr nicht wieder ein).
Uebrigens ist die Luecke, wie das Bild auch zeigt, abhaengig von der Entfernung bei der Umkehr. Bei doppelt so grosser Entfernung von der Erde aber gleichen Geschwindigkeitsverhaeltnissen wird sie doppelt so gross. Sie hat nichts mit der Staerke oder Dauer der Beschleunigung beim Umkehren zu tun.
Der Denkfehler ist also anzunehmen, dass die Situation der Zwillinge symmetrisch ist. Das ist sie nicht. Zwar verhalten sich die relativen Beschleunigungen der beiden symmetrisch zueinander, aber die von Stella ist mit einem echten Wechsel des Inertialsystems verbunden, merkbar an dem Andruck bei der Beschleunigung zwecks Bewegungsumkehr, waehrend die von Theresa keinen Wechsel des Inertialsystems beinhaltet (als das die Erde hier naeherungsweise angesehen wird). Sie merkt ja auch auf der Erde nichts von einer Bewegungsumkehr.
Haetten wir Drillinge, also etwa noch eine Ursula, die in der entgegengesetzten Richtung davonfliegt wie Stella, mit einem exakt symmetrischen Beschleunigungsprogramm, so waeren bei der Rueckkehr Ursula und Stella gleich alt (und beide juenger als Theresa). Dass tatsaechlich Stella juenger bleibt, laesst sich ohne Rechnung nur aus dem Diagramm zwilling1 sehen, da wir in zwilling2 ja nicht unmittelbar aus der Zeichnung entnehmen koennen, wie gross die Summe von 2 mal \Delta t* plus der Luecke im Vergleich zu 2 \Delta t' ist. Das zeigt, dass es im allgemeinen einfacher ist, Physik in Inertialsystemen zu beschreiben als in Nichtinertialsystemen (das Bezugssystem von Stella ist nicht ueber die gesamte Dauer der Reise inertial).
Inertialsysteme koennen auch als solche Bezugssysteme definiert werden, in denen die physikalischen Gesetze eine besonders einfache Form haben.
3.7 Das Duell mit Tachyonenpistolen
Bis jetzt habe ich noch nichts zu E = mc^2 gesagt. Und ich habe auch nicht vor, diesbezueglich tiefer einzusteigen. Man kann die Massenformel der Relativitaetstheorie auch mit Minkowski-Diagrammen ableiten, aber es erfordert an einer Stelle einen "leap of faith", den ich den Lesern nicht zumuten moechte.
Zudem kann man aus der Massenformel kann nicht schliessen, dass Ueberlichtgeschwindigkeiten unmoeglich seien. Nimmt man etwa an, dass es Teilchen mit imaginaerer Ruhmasse gibt (das sind die Tachyonen), dann muessen die sogar schneller als das Licht sein, um eine reelle Energie zu haben.
Allerdings haette ihre Existenz eigenartige Konsequenzen, wenn das Bild der Raumzeit, das uns die spezielle Relativitaetstheorie gibt, richtig ist. Das soll anhand einer kleinen science-fiction-Geschichte illustriert werden.
Wir setzen voraus, dass Tachyonen in neuartigen Waffen als toedlicher Energiestrahl benuetzt werden koennen. Diese Waffen sind gerade vor Stellas Flug zum Alpha Centauri erfunden worden. Alf und Bert sind zwei junge Maenner, die um Stellas Gunst bemueht sind. Nur einer kann aber mit nach Alpha Centauri. Deshalb beschliessen sie, sich zu duellieren.
 |
| Bild tachyonen |
|---|
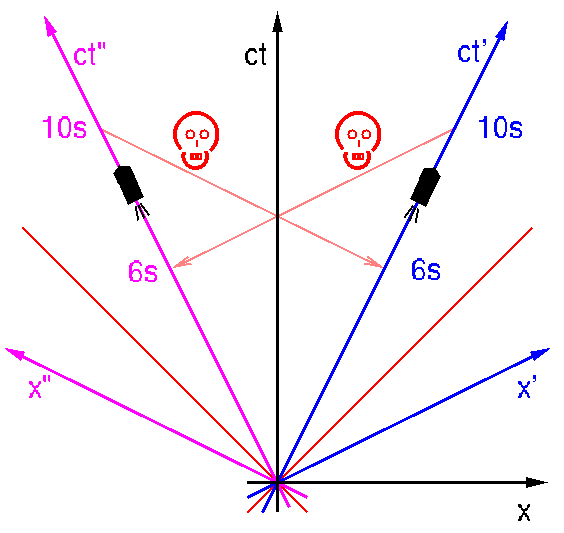
Das Duell geht so: sie fliegen mit Raumscootern, das sind die kleinen Raketen in Bild tachyonen, 10 Sekunden lang auseinander. Dann drehen sich beide um und schiessen mit ihren Tachyonenpistolen aufeinander.
Die Raumfluege verlaufen im Rahmen der normalen Physik. Die Relativgeschwindigkeit der beiden sei (+-)4/5 c, dann ist der Zeitdilatationsfaktor 3/5. Die Tachyonen sollen so schnell sein, dass sie sich praktisch in Nullzeit ausbreiten, d.h. im Diagramm fliegen sie nahezu parallel zur Achse x' bzw. x" (die ja gleichzeitige Ereignisse verbinden). Dass die beiden Raumschiffe langsamer als das Licht sind, sieht man daran, dass die Steigungen ihrer Weltlinien (betragsmaessig) groesser als die des Lichtkegels sind. Die Tachyonen sind schneller als das Licht und ihre Weltlinien haben eine betragsmaessig kleinere Steigung als die des Lichts.
Unsere Helden drehen sich also jeweils nach 10 Sekunden um und ballern los. Alf, dessen Weltlinie blau ist, trifft gut. Bert wird also von Alfs Strahl getoetet, und nach Alfs Rechnung sind auf Berts Uhr erst 6 Sekunden vergangen. Bert rechnet aber anders. Da fuer ihn Alfs Zeit langsamer geht, hat Alf noch nicht geschossen, wenn seine 10 Sekunden um sind. Und Bert schiesst auch gut. Er toetet also Alf zu einem Zeitpunkt, wo auf dessen Uhr 6 Sekunden um sind. Dann kommt Alf aber gar nicht mehr dazu, ihn zu erschiessen. Das gleiche Argument gilt aber auch fuer Bert. Da Alf auf ihn schiessen kann, bevor seine 10 Sekunden um sind (nach Alfs Uhr), wird er schon nach 6 Sekunden toedlich getroffen und kommt nicht mehr dazu, Alf zu erschiessen. Da er aber Alf nach 6 Sekunden (auf dessen Uhr) trifft, kann dieser ihn nicht mehr erschiessen. Und so weiter, ad infinitum.
Ein echtes Paradox. Und wir sehen auch, dass im schwarzen Koordinatensystem (dem des Schiedsrichters) die Tachyonenstrahlen in die Vergangenheit gehen. Es handelt sich also um ein Zeitparadox mit entsprechender Kausalitaetsverletzung. Jeder erschiesst den anderen, bevor der ihn toeten kann. Da dann aber jeder getoetet wird, bevor er schiessen kann, erschiesst keiner den anderen, bevor die Waffen benuetzt werden. Dann aber kann wieder geschossen werden, und man toetet sich...
Es gibt verschiedene Moeglichkeiten, diesen Konsequenzen auszuweichen. Die einfachste, allgemein anerkannte, ist, ueberlichtschnelle Signale und damit Tachyonen auszuschliessen. Warum ist das notwendig und hinreichend? Ein ueberlichtschnelles Signal hat eine Trajektorie, die "flacher" ist als der Lichtkegel. Es kann also ein Bezugssystem gefunden werden, in dem seine Weltlinie die x'-Achse eines sich unterlichtschnell bewegenden Beobachters ist. In diesem Bezugssystem bewegt sich das Signal unendlich schnell. Fuer einen Beobachter, der noch ein bisschen schneller fliegt, geht es sogar in die Vergangenheit, womit prinzipiell eine Situation wie die eben fuer Alf und Bert geschilderte moeglich wird (dazu sind also nicht extrem schnelle Tachyonen noetig -- es reicht, wenn sie nur wenig schneller sind als das Licht). Wenn aber alle Signale unterlichtschnell sind, kann keines parallel zur x'-Achse eines Beobachters laufen, weil diese Achsen fuer unterlichtschnell bewegte Beobachter alle flacher verlaufen als der Lichtkegel. Damit ist ein Paradoxon wie das geschilderte ausgeschlossen. Man kann zeigen, dass ein unterlichtschnelles Signal in allen Bezugssystemen unterlichtschnell ist.
Das ist also der Grund, warum die spezielle Relativitaetstheorie ueberlichtschnelle Signale (und damit auch Reisen) ausschliesst (wenn das Kausalprinzip gilt -- dazu spaeter mehr). Es ist nicht so wichtig, dass bei Annaeherung an die Lichtgeschwindigkeit Massen unendlich gross werden (das koennte man ja umgehen, indem man die "Lichtbarriere durchtunnelt", also nie exakt mit Lichtgeschwindigkeit fliegt). Aber, und das ist der springende Punkt, wenn die von der Relativitaetstheorie behauptete Struktur der Raumzeit richtig ist, dann ist es voellig unabhaengig davon, auf welche Weise man Ueberlichtgeschwindigkeit erreicht. Man kann sie fuer das Senden von Signalen in die Vergangenheit verwenden und damit Paradoxa produzieren.
Welche anderen Moeglichkeiten gibt es, dem Paradoxon auszuweichen? Immerhin sind in der Physik Tachyonen ja ernsthaft in Erwaegung gezogen worden. Eine Loesung waere, dass man bei diesen Teilchen nicht zwischen Emission und Absorption unterscheiden koennte. Dann liessen sich die Tachyonenstrahlen von Alf und Bert uminterpretieren: die pinken Pfeile muessten aus der Sicht des schwarzen Beobachters in ihrer Richtung umgedreht werden und wuerden nun in die Zukunft gehen. Allerdings waere eine Pistole, bei der man nicht entscheiden kann, ob sie schiesst oder gerade einen Treffer kassiert, nicht sehr nuetzlich... Ausserdem haetten die Tachyonen dann je nach Bezugssystem auch mal negative Energien, was andere unangenehme Konsequenzen haette...
Man koennte auch (motiviert durch Erfahrungen mit der Quantenmechanik) daran denken, dass Tachyonen nur bedingt kontrollierbar sind. Doch das genuegt nur dann zur Vermeidung des Paradoxons, wenn die bedingten Kontrollen der beiden Strahlen korreliert sind. Denn bei unabhaengigen Ergebnissen der Schiessversuche wuerde, auch wenn jeder der beiden Schuetzen nur mit einprozentiger Wahrscheinlichkeit einen Tachyonenstrahl zustandebringt (was die Nutzung als Waffe de facto ausschloesse), doch mit einer Wahrscheinlichkeit von 1/10000 ein Paradoxon zustandekommen. Was es braucht, ist die Verhinderung eines Treffers aufgrund der Tatsache, dass die beiden Tachyonenstrahlen einander begegnen! Man ist schon geneigt, Korrelationen dieser Art ins Reich der Magie zu verweisen.
Ferner liesse sich das Paradoxon auch vermeiden, wenn man die Willens- oder besser Handlungsfreiheit der Protagonisten verneint. Wenn sie nicht frei sind zu schiessen, kann immer einer irgendwie daran gehindert sein oder danebenschiessen (was heisst kann: muss). Welche Gesetze aber dies regeln sollen, bleibt schleierhaft...
Einen etwas befriedigenderen Weg, der aber auf eine Abschaffung der speziellen Relativitaetstheorie hinauslaeuft, werde ich im letzten Abschnitt des Kurses besprechen.
Die naechste Unterrichtseinheit wird neben der Aufloesung des Raumschiffpuzzles eine kurze Diskussion des Kausalitaetsprinzips beinhalten. Dann kommt meine Perry-Rhodan-Geschichte, die illustrieren soll, wie die Relativitaetstheorie bei grossen Entfernungen massiven Einfluss auf das Bild hat, das man sich vom "jetzigen Augenblick" machen muss und dass da schon sehr kleine Geschwindigkeiten, wie die Umlaufsgeschwindigkeit der Erde um die Sonne, eine Rolle spielen.
Klaus Kassner
Institut fuer Theoretische Physik / Computerorientierte Theor. Physik
Otto-von-Guericke-Universitaet Magdeburg
Postfach 4120 / D-39016 Magdeburg